Capacitance:
The capacitance of capacitor is expressed as AC capacitance by measuring impedance and separating factors. Also, the AC capacitance depends upon frequency, voltage and other measuring methods. 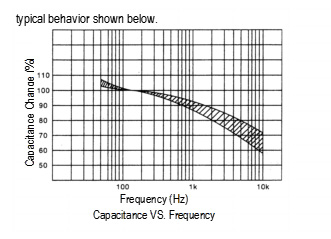In fact, JIS C 5101 prescribes that the series capacitive factor of an equivalent series ( ) circuit shall be the capacitance measured at a frequency of 120 Hz and applying a maximum AC voltage of 0.5Vrms with a DC bias voltage of 1.5 or 2.0 V to aluminum electrolytic capacitors. The capacitance of an aluminum electrolytic capacitor becomes smaller with increasing frequency. See the typical behavior shown below.
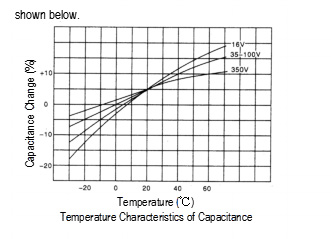
The capacitance value is highly dependent upon temperature and frequency. As the temperature decreases, the capacitance becomes smaller. See the typical behavior shown below.
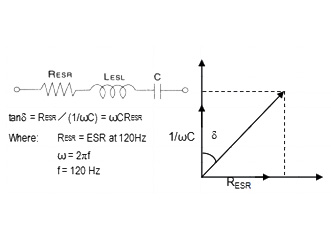
On the other hand, DC capacitance, which can be measured by applying a DC voltage, shows a slightly larger value than the AC capacitance at a normal temperature and has the flatter characteristic over the temperature range. tanδ (tangent of loss angle or dissipation factor) The tanδ is expressed as the ratio of the resistive component (RESR) to the capacitive reactance (1/ωC) in the equivalent series circuit . Its measuring conditions are the same as the capacitance.
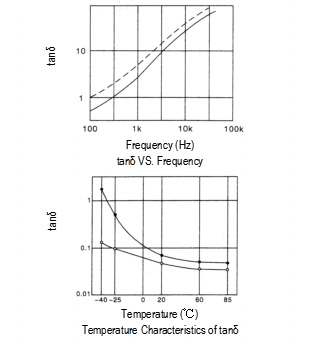
The tanδ shows higher value as the measured frequency increases and the measured temperature decreases.
Equivalent series resistance (ESR):
The ESR is the series resistance consisting of the aluminum oxide layer, electrolyte/separator combination and other resistance related factors, foil length. Foil surface area and others.
The ESR value depends upon the temperature. Decreasing the temperature makes the resistivity of the electrolyte increase and leads to increasing ESR. As the measuring frequency increases, the ESR decreases and reaches an almost constant value that mainly dominates the frequency-independent resistance relating electrolyte/ separator combination.
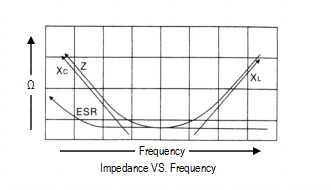
Impedance (Z):
The impedance is the resistance of the alternating current at a specific frequency. It is related to capacitance [C] and inductance [L] in terms of capacitive and inductive reactance, and also related to the ESR. It is expressed as following:
Z = √[ESR2 + (XL - XC)2]
Where:
XC = 1/ωC = 1/2πfC
XL = ωL = 2πfL
As shown below, the capacitive reactance (XC) dominates at the range of low frequencies, and the impedance decreases with increasing frequency until it reaches the ESR in the middle frequency range. At the range of the higher frequencies the inductive reactance (XL) comes to dominate, so that the impedance increases when increasing the measuring frequency.